libMoM-0.11: Example Problems

Examples

We consider four illustrative examples that show the implementation of different terms in the moments equation. The first example is a 1D Brownian coagulation example. This example illustrates the use of source terms from collisional integrals. Example 2 is a 1D Fokker Planck example that shows growth and diffusion terms. Example 3 is a 2D version of the Fokker Planck equation. Example 4 is a moments matching example where the CDF is estimated from the moments. The examples and results are described in much greater detail here .

Example 1 : Brownian coagulation of an aerosol population

The input parameters are first defined in a file (see the Brownian Coagulation Input File). The file is written so that it can be referenced using GetPot. The input file is read in here. In this case the moments source terms in the moments equation is given by:

$\begin{eqnarray} \frac{1}{2} \sum_{i=1}^{N_Q}\sum_{j=1}^{N_Q} \left[ (\tilde{\xi}_i + \tilde{\xi}_j)^k - \tilde{\xi}_i^k - \tilde{\xi}_j^k \right] K_c (\tilde{\xi}_i, \tilde{\xi}_j) W_i W_j \end{eqnarray}$

The user needs to enter this source term in a separate program. The fully documented code is given in User Defined Function. The main program is executed in Main Program. The outputs are processed also in the user interface program, User Defined Function. If 3 quadrature points are used, then the program is run as:

 > ./Brownian_Coagulation 1 3 Brownian_Coagulation.inp

Example 2 : 1D Fokker planck equation

The input parameters are first defined in a file (see the 1D Fokker Planck Input File). The file is written so that it can be referenced using GetPot. The input file is read in here. In this example both source terms and growth terms are present. The source terms are:

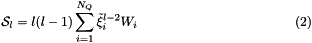
$\begin{eqnarray} \mathcal{S}_{l} = l (l-1) \sum_{i=1}^{N_Q} \tilde{\xi}_{i}^{l-2} W_i \label{eq:1d_Fokker_Planck_source_term} \end{eqnarray}$

The growth terms for each quadrature point are:

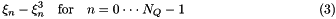
$\begin{eqnarray} \xi_n - \xi_n^3 \quad \text{for} \quad n = 0 \cdot \cdot \cdot N_Q -1 \end{eqnarray}$

The user needs to enter this source and growth terms in a separate program. The fully documented code is given in User Defined Function. The main program is executed in Main Program. The outputs are processed also in the user interface program, User Defined Function. If 8 quadrature points are used, then the program is run as:

 > ./Fokker_Planck_1D 1 8 Fokker_Planck_1D.inp

Example 3 : 2D Fokker planck equation

The input parameters are first defined in a file (see the 2D Fokker Planck Input File). The file is written so that it can be referenced using GetPot. The input file is read in here. In this example there are two variables and there is a choice as to which one is the principal variable for which a larger number of higher order moments are evolved. Let us choose 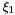$\xi_1$ as the principal variable. Then the source term can be written as:

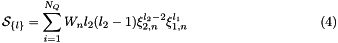
$\begin{eqnarray} \mathcal{S}_{\{l\}} = \sum_{i=1}^{N_Q} W_n l_2 (l_{2}-1) \xi_{2,n}^{l_2-2} \xi_{1,n}^{l_1} \label{eq:2d_Fokker_Planck_source_term} \end{eqnarray}$

Since 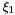$\xi_1$ is chosen as the principal variable the first index 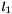$ l_1 $ is associated with 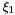$\xi_1$ . The growth terms are:

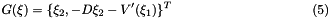
$\begin{eqnarray} G( \mathbf{\xi} ) = \{ \xi_2, - D \xi_2 - V' (\xi_1) \}^{T} \label{eq:growth_terms_2d} \end{eqnarray}$

Since 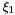$\xi_1$ is chosen as the principal variable, the growth terms for this variable needs to be entered first. The fully documented code where the user enters these terms are provided is given in User Defined Function. The main program is executed in Main Program. The outputs are processed also in the user interface program, User Defined Function.

Example 4 : CDF reconstruction (Design Fire Example)

The input parameters are first defined in a file (see the Design Fire Input File). The file is written so that it can be referenced using GetPot. The input file is read in here. The computation of the moments of the quantity of interest is performed in here. The main program (Main Program) includes calls to the moment matching algorithm. If fmkl is chosen as the parametrisation of the GLD (the other option is rs), then he program is executed as follows:

 > ./Design_Fire 1 3 Design_Fire.inp fmkl