In this section, we provide theoretical information on the moment methods and moment matching algorithms. This is only in order to aid the user in the use of the software. The theory is treated in much greater length in the paper available in here [1].
Suppose that 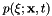 is a probability density function distributed in space
is a probability density function distributed in space 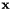 and time
and time 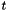 with internal (random) variables
with internal (random) variables 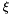 . The general PBE governs the evolution of the PDF in
. The general PBE governs the evolution of the PDF in 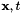 and internal variables
and internal variables 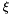 , as derived in [2].
, as derived in [2].
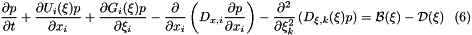
The above equation describes the evolution in both external (physical) space ( 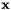 ) as well as internal space (
) as well as internal space ( 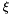 ). The velocity in physical space is
). The velocity in physical space is  and the velocity in internal space, also referred to as the growth term, is
and the velocity in internal space, also referred to as the growth term, is 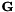 . The fourth and fifth terms in the left hand side model the diffusion in physical space and internal space. These terms account for the diffusive transport in external space and fluctuations of the system in the internal spaces caused by random external influences.
. The fourth and fifth terms in the left hand side model the diffusion in physical space and internal space. These terms account for the diffusive transport in external space and fluctuations of the system in the internal spaces caused by random external influences.  and
and 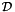 are the birth and death terms and can be treated as source terms.
are the birth and death terms and can be treated as source terms.
The moments are averages of 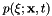 over the internal state space
over the internal state space 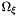 . If
. If 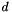 is the dimension of the internal space represented by the
is the dimension of the internal space represented by the 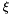 coordinate then:
coordinate then:
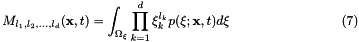
The method of moments involves taking moments of both sides of the population balance equation to give us the following system of equations indexed by the 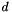 -tuple
-tuple 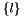 .
.
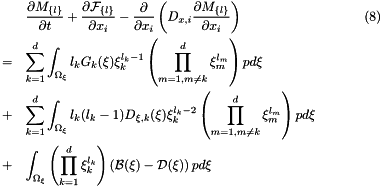
with
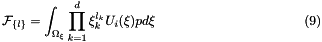
The quadrature based moment method involves approximating the moments using Gaussian quadrature formula:
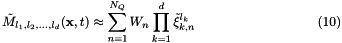
In the above quadrature formula 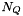 is the number of quadraure points and
is the number of quadraure points and 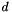 is the dimension of the space over which the PDF is defined (the internal space),
is the dimension of the space over which the PDF is defined (the internal space), 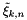 is the
is the  quadrature point for the
quadrature point for the 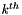 variable and
variable and  is the weight associated with the
is the weight associated with the  quadrature point. We denote the approximate moments by
quadrature point. We denote the approximate moments by 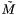 . Note that there are a total of
. Note that there are a total of 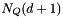 quadrature points and weights and consequently a set of
quadrature points and weights and consequently a set of 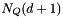 moments need to be evolved to compute the quadrature points and weights at each step. With the application of the quadrature formula in the moments equation we get:
moments need to be evolved to compute the quadrature points and weights at each step. With the application of the quadrature formula in the moments equation we get:
![\begin{eqnarray} &&\frac{\partial \tilde{M}_{\{l\}}}{\partial t} + \frac{\partial \tilde{\mathcal {F}}_{\{l\}}}{\partial x_i} - \frac{\partial}{\partial x_i} \left( D_{x,i} \frac{\partial \tilde{M}_{\{l\}}}{\partial x_i} \right) \label{eq:closed_moment_eqs} \\ \notag &=& \sum_{k=1}^{d} \left[\sum_{n=1}^{N_{Q}} W_n l_k G_k(\mathbf{\tilde{\xi}}) \tilde{\xi}_{k,n}^{l_k-1}\left( \displaystyle\prod_{m = 1, m \neq k}^d \tilde{\xi}_{m,n}^{l_m} \right) \right] \\ \notag &+& \sum_{k=1}^{d} \left[ \sum_{n=1}^{N_{Q}} W_n l_k(l_{k} - 1) D_{\xi,k}(\mathbf{\tilde{\xi}}) \tilde{\xi}_{k}^{l_{k}-2}\left( \displaystyle\prod_{m = 1, m \neq k}^d \tilde{\xi}_m^{l_m} \right) \right] \\ \notag &+& \sum_{n=1}^{N_{Q}} W_n \left( \displaystyle\prod_{k=1}^d \tilde{\xi}_k^{l_k} \right) \left( \mathcal{B}(\mathbf{\tilde{\xi}}) - \mathcal{D} (\mathbf{\tilde{\xi}}) \right) \end{eqnarray}](form_32.png)
In order to solve this equation the user needs to supply the source terms on the right hand side. The user also needs to supply the growth terms for the 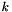 dimensions, evaluated at the quadrature points
dimensions, evaluated at the quadrature points 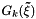 . Note that unlike the source terms, moments do not have to be taken of the growth terms. Various examples where this equation is solved is given in Example Problems section.
. Note that unlike the source terms, moments do not have to be taken of the growth terms. Various examples where this equation is solved is given in Example Problems section.
The method that we have outlined can be used to propagate the moments of an underlying probability density function (PDF) (or number density function) whose evolution is governed by the population balance equation (PBE). Frequently in numerous applications the form of the PDF or the cumulative distribution function (CDF) is required. The moments by itself do not give sufficient information to reconstruct the CDF. An infinite number of distribution functions can have the same moments. Additional hypotheses are required about the shape of the PDF or the statistical family to which the PDF belongs.
In [3], the moment matching method is presented in which the moments are matched with the moments of the Generalized Lambda family of Distributions (GLD). Four moment based parameters, the mean, variance, skewness and Kurtosis of the GLD can be computed with different parametrizations of the quantile function for the family. A deterministic parameter estimation problem is solved by minimizing the least square difference between the available moments and the moments of the GLD. We choose the GLD as it is a versatile family of distributions that can capture the shapes of a large number of commonly used distributions. We implement the algorithm described in [4]. Details on the algorithm can be found in this paper .
The main library is written in C++. All the basic mathematical routines are used from the GSL library. C++ wrappers are created for all the GSL functions. The directory structure is available in the the Directories section. The detailed class documentation can be found in the Classes section. Worked out examples are included in the distribution. A description of worked out examples can be found in Example problems.
[1]. Upadhyay, R.R., Ezekoye, O. A., libMoM: a library for stochastic simulations in engineering using statistical moments. Engineering with Computers, DOI: 10.1007/s00366-011-0219-9.
[2]. Ramkrishna, D., Population Balances: Theory and Applications to Particulate Systems in Engineering. Academic Press, San Diego (2000)
[3]. Karian, Z.A., Dudewicz, E.J., Fitting statistical distributions: the generalized lambda distribution and generalized bootstrap methods, CRC Press, Boca Raton (2000)
[4]. Lakhany, A., Mausser,H., Estimating the Parameters of the Generalized Lambda Distribution. Algo Res Quart, 3(3), 47-58 (2000)
 1.7.2
1.7.2